games101-lecture14 笔记
Today
- Acceleration 加速结构:使用AABB来加速光线追踪
- Uniform grids
- Spatial partitions
- Basic radiometry(辐射度量学)
- 进阶:不同于Whitted-Style的光线追踪
光线追踪加速结构
均匀网格方案:Uniform grids
预处理:构建加速网格
找一个包围盒,在包围盒中构建均匀网格,记录每一个与物体相交的网格
光线与场景求交
射出一道光线,让光线与格子求交,若格子内存在物体,再让光线与物体求交:光线与格子求交是快速的,而与实际物体求交是很慢的,通过这样的理念来优化
经验告诉我们
当格子数等于C * 对象数时,结果会比较好;三维空间下常数C可以取27
缺陷
当细节物品在空间中分布不均匀时,存在大规模集中、大规模空白:”Teapot in a stadium” problem
*在一些场景下还是好用的,仍有在使用
空间划分 Spatial partitions
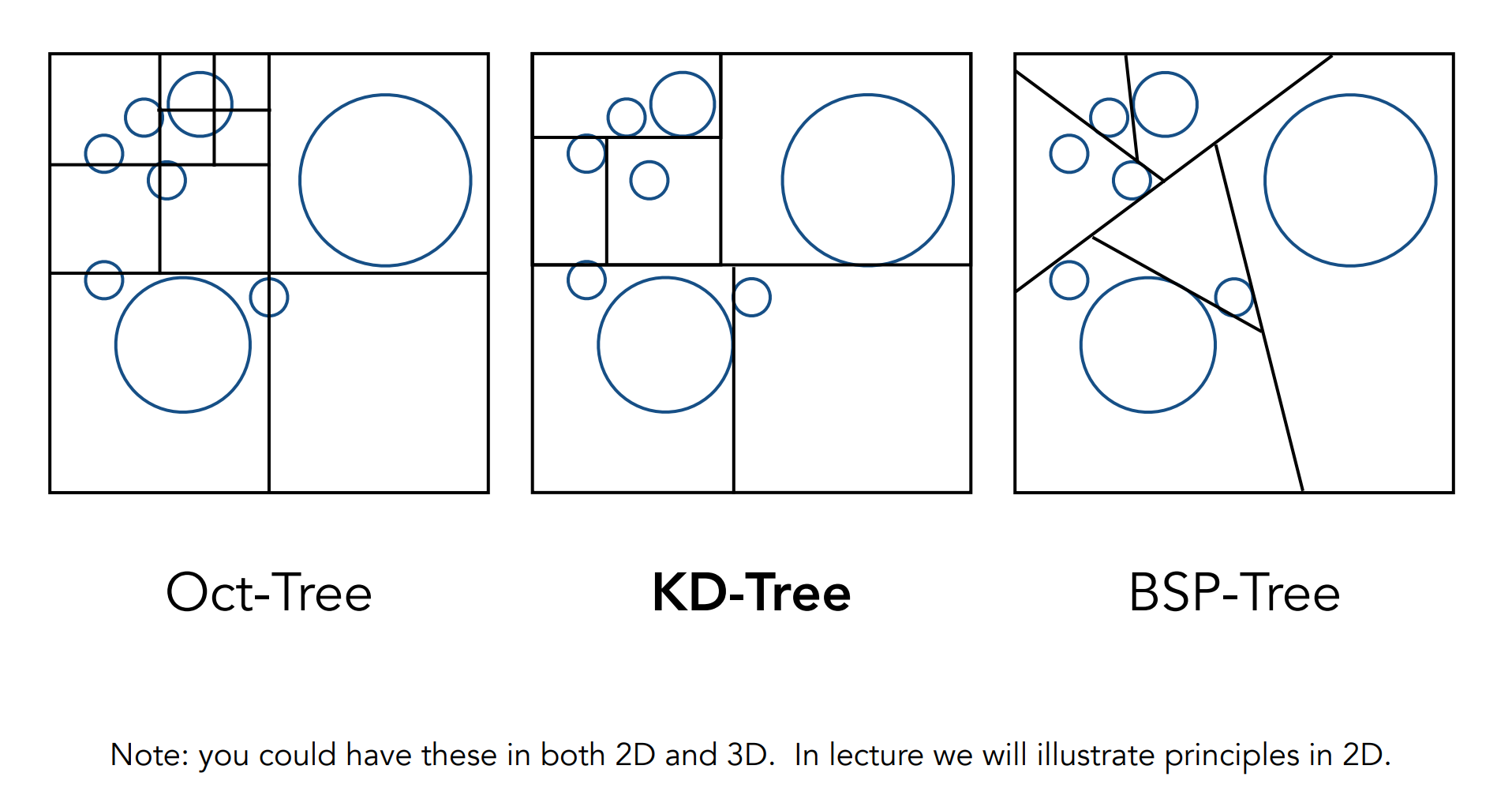
Oct-Tree 八叉树:三维空间划分为8份,在格子类数量足够少,或者划分次数足够多时不再划分。
想让空间得到划分,但是不想随着维度不断提高子节点指数级增长,发明了KD-Tree。
KD-Tree(本次重点):每次对格子只进行一次划分,划分为两个区域;每次进行划分时采取与上一次不同的轴向,可以得到尽可能均匀的划分结果。(Root: axis-x,layer1: axis-y,layer2: axis-z)
BSP-Tree:同样是空间二分方法,区别在于不是水平竖直地进行划分
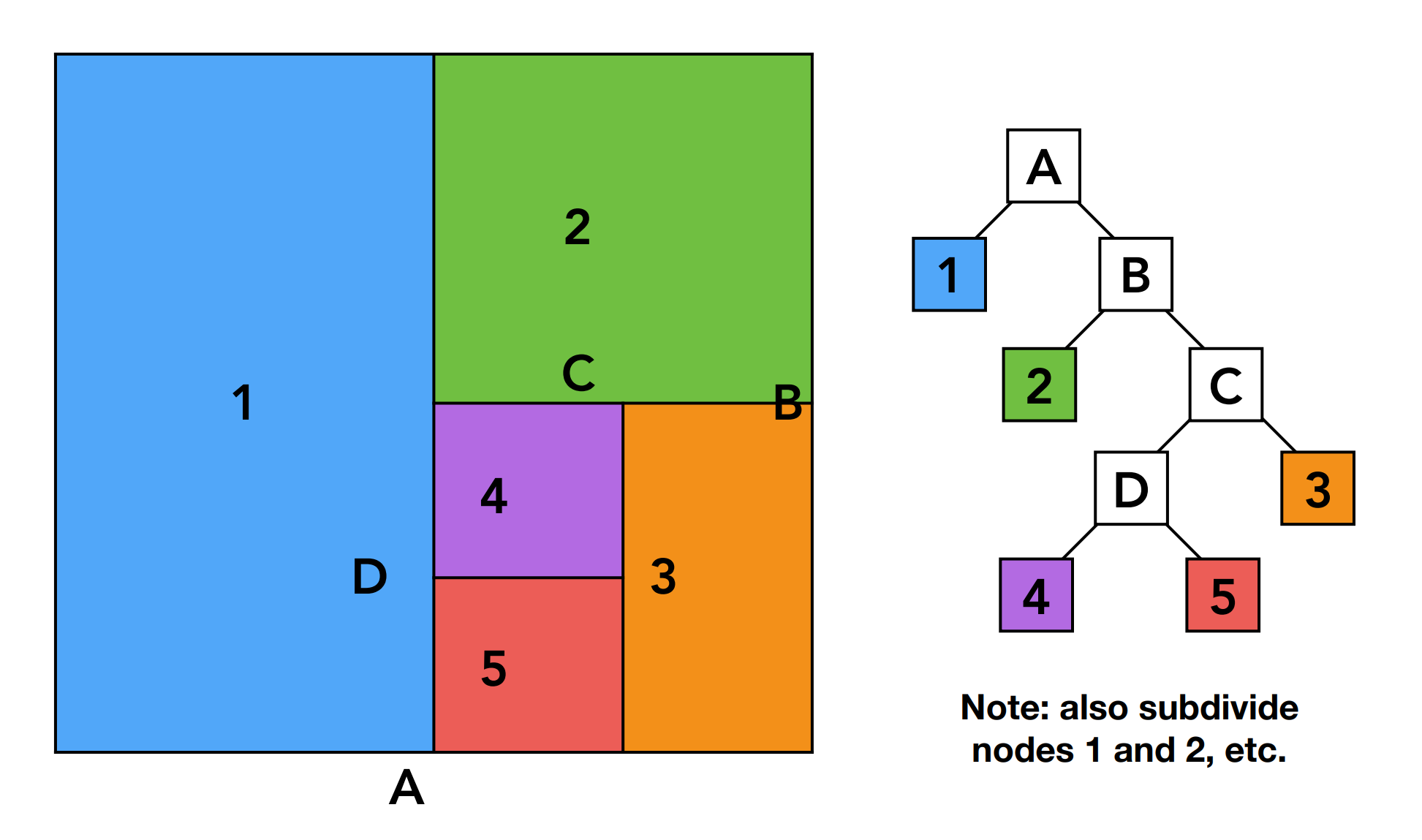
KD-Trees 数据结构
中间节点存储(A,B,C):
- 划分使用的轴(x, y, z)
- 划分的位置(在轴向上的什么地方划分)
- 所有子节点指针
- 注意中间节点不存储对象(objects)
叶子节点存储(1,2,3):
- 对象的列表存储
遍历KD-Tree进行求交
如果光线与中间节点代表的区域相交,就意味着光线也要与中间节点划分出的子节点判定相交;递归此过程,最后达到一个叶子节点,就和叶子节点中的所有对象求交。
进阶问题
如何判定对象与包围盒的相交关系
需要考虑三角形与盒子的求交
空间划分涉及的问题,如何判断对象是否在某个划分的格子内?
或者,某个划分出来的各自内有哪些对象?
虽然有现成的算法,但是不容易写对,在一些情境下容易犯错。
对象重复出现在不同的划分格子中
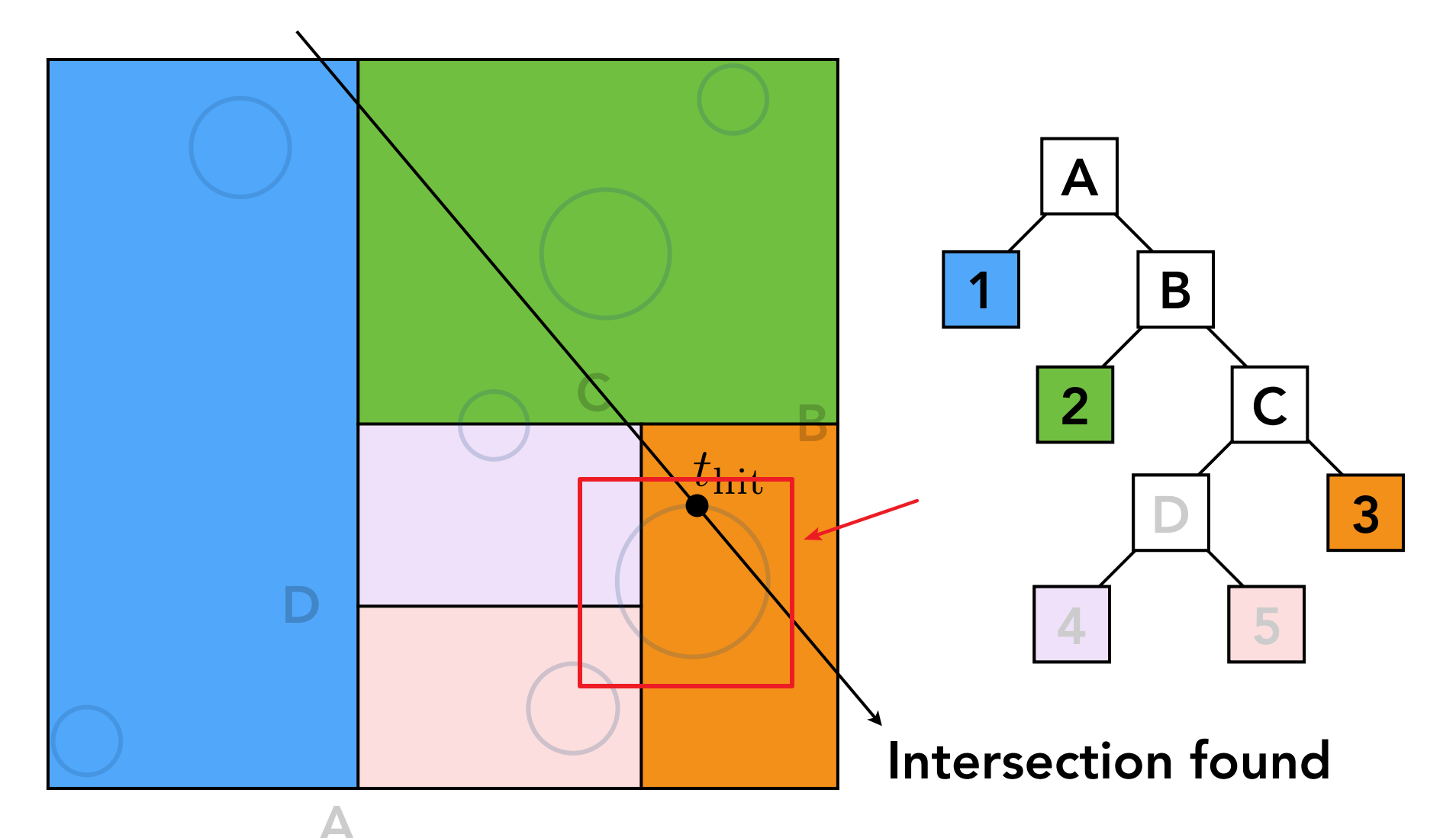
如图中的这个圆,出现在分区3,4,5内,即这三个分区内会重复出现这个圆
Object Partitions & Bounding Volumn Hierarchy(BVH)
解决了上述KD-Tree的两个问题,目前图形学更受欢迎的结构。
划分的不是空间,而是把物体分为两个部分;如下例,把一个盒子内的三角形分成了两个部分(基于某种标准),之后再分别计算两个部分的包围盒。
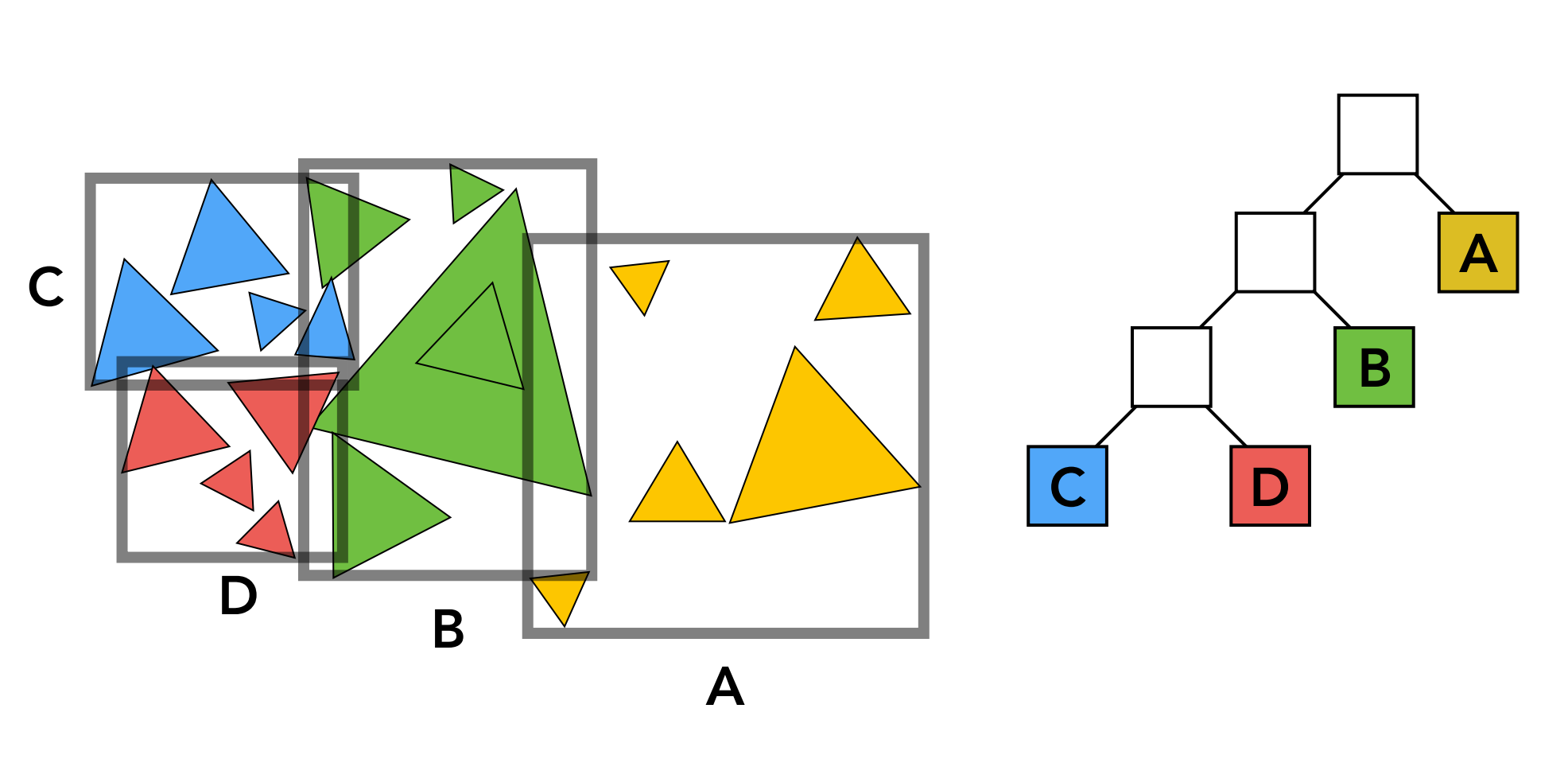
特性:
- 一个物体只可能出现在一个格子(分区)里
- 求所有三角形包围盒算法也很简单,不用计算三角形和盒子的相交关系
- 每个分区可能有相交:关于怎么将其划分为两个部分,很有讲究,有相关的研究
详解做法:
- 找到一个包围盒
- 递归地将其内部的对象分为两个子集
- 重新计算子集地包围盒
- 适当地停止(子集数量足够少,划分次数足够多)
- 将物体存储在每一个叶子节点中
如何划分一个节点/分区:
- 选择一个划分的维度
- 经验谈 #1:沿着分区里最长的轴向划分,让它变短,更容易形成均匀分区
- 经验谈
#2:取”中间”的物体:在即将划分的轴向上,进行排序(若划分x轴,则对x坐标进行排序),取中位数序号(n/2)的物体进行划分,可以让两个子分区的数量接近,从而让树的深度更小,搜索更快
- 无序数组中求第i大的数,实际上可以不需要排序\(O(nlgn)\):快速选择算法 \(O(n)\) → 快速排序算法的启发,算法中Partition做完后,只对其中一边进行操作
BVH的数据结构
中间节点存储:
- 包围盒
- 子节点的指针
叶子节点存储:
- 包围盒
- 包含对象的列表
两类划分的比较
空间划分:KD-tree
- 将空间划分为不重叠的两个分区
- 一个物体可能存在于多个分区内
物体划分:BVH
- 将对象划分为不相交的子集
- 不同集合的包围盒可能在空间上重叠
因为实现容易,效率也不错,BVH得到了更大的应用
加速结构完成后,光线和场景的求交就能在很短的时间内完成
辐射度量学 Radiometry
动机 motivation
为什么需要辐射度量学?
来自过去的疑问:
- Blinn-Phong模型中的光线强度 \(I=10\),单位是?
- Whitted style的光线追踪看起来是正确结果吗?
Blinn-Phong模型有许多简化,人为设置的内容,而辐射度量学可以对光的行为提供精确描述
内容
- 测度系统与光照的单位
- 对光的空间属性的精确描述
- 光照的若干属性:Radiant flux, intensity, irradiance, radiance
- 通过物理上正确的方式(a physically correct manner)来进行光照计算
Radiant Energy and Flux (Power)
Radiant energy:电磁辐射的能量,单位焦耳(J)
\[ \begin{equation}Q[\mathrm{~J}=\text { Joule }]\end{equation} \]
Radiant flux(power):单位时间的能量,energy per unit time,得到功率,单位瓦特(W),图形学使用的另一个单位(lumen 流明)
\[ \begin{equation}\Phi =\frac{\mathrm{d} Q}{\mathrm{~d} t}[\mathrm{~W}=\mathrm{Watt}][\mathrm{lm}=\text { lumen }]^*\end{equation} \]
另一种flux的理解:单位时间内通过感光平面的光子数量
其他的重要物理量
- 光源辐射出的能量:Radiant Intensity
- 表面接收到的能量:Irradiance
- 光线沿着射线的传输:Radiance
Radiant Intensity
定义:power per uint solid angle,每单位立体角的功率,单位 candela
\[ \begin{equation}\left[\frac{\mathrm{W}}{\mathrm{sr}}\right]\left[\frac{\mathrm{lm}}{\mathrm{sr}}=\mathrm{cd}=\text { candela }\right]\end{equation} \]
什么是立体角?
角度的定义,弧长除以半径,弧度制。
立体角:弧度在三维空间的延伸。在三维空间的球中找一个锥,这个锥在球上有一个球表面积,将这个面积除以球半径的平方。因为球表面积是 \(4\pi{r}^2\),所以球有\(4\pi\)立体角(steradians)
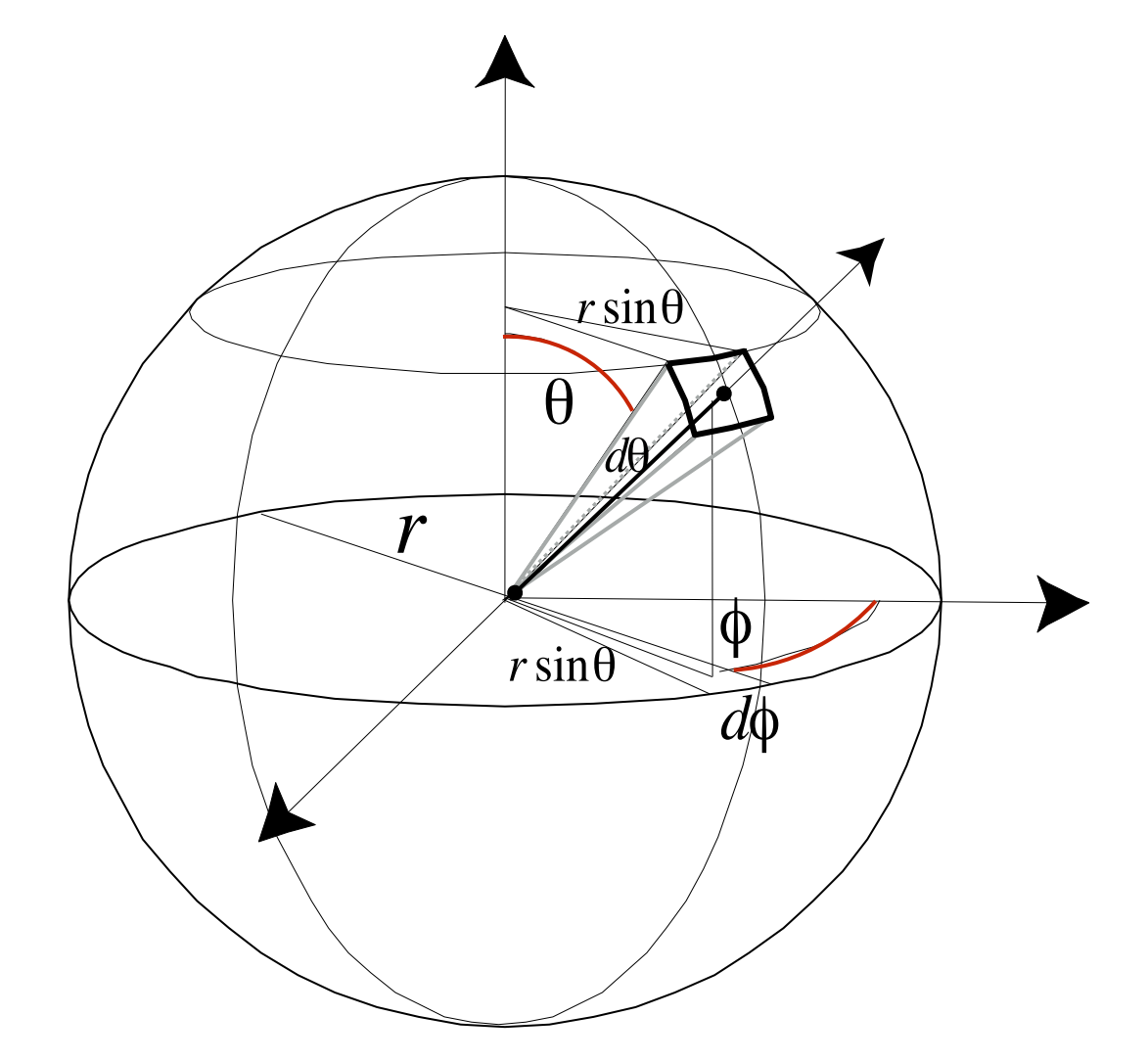
单位立体角(Differential Solid Angles):
\[ \begin{equation}\begin{aligned}\mathrm{d} A & =(r \mathrm{~d} \theta)(r \sin \theta \mathrm{d} \phi) \\& =r^2 \sin \theta \mathrm{d} \theta \mathrm{d} \phi\end{aligned}\end{equation} \]
\[ \begin{equation} \mathrm{d} \omega=\frac{\mathrm{d} A}{r^2}=\sin \theta \mathrm{d} \theta \mathrm{d} \phi \end{equation} \]
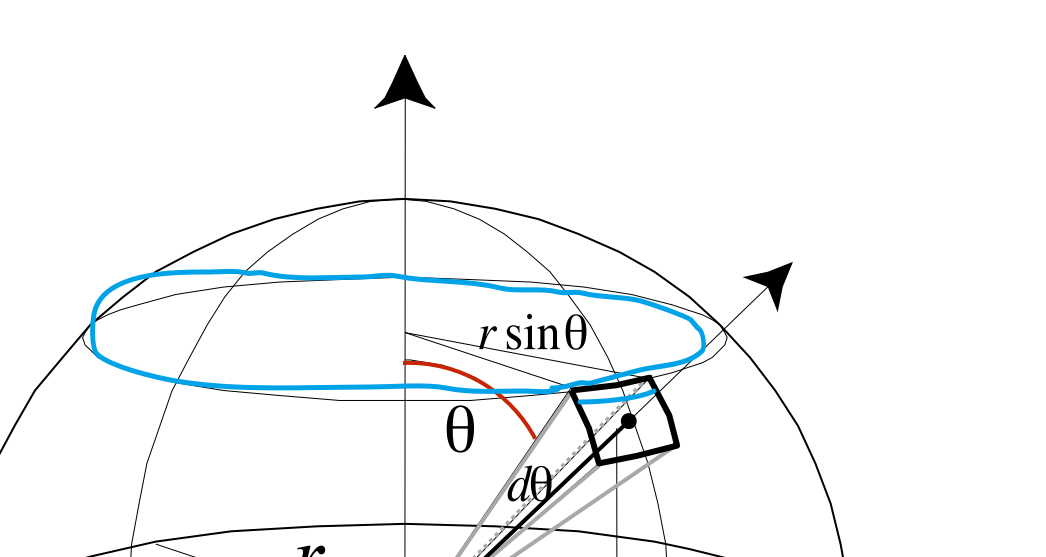
为什么是面积微分\(\mathrm{d} A\) 的一个因数是 \(r \sin \theta \mathrm{d} \phi\),可以看蓝线这个圆上的弧
回头看Intensity的定义
intensity,即为power在某一个方向的微分。所以如果对于均匀的点光源,有以下:
\[ \begin{equation} I = \frac{\Phi}{4\pi}\end{equation} \]